Données appariées dans les statistiques

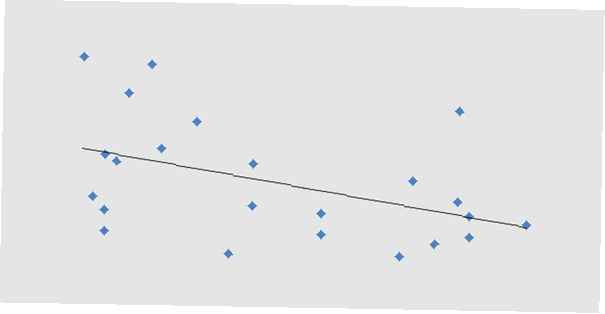
Les données appariées dans les statistiques, souvent appelées paires ordonnées, se réfèrent à deux variables chez les individus d'une population qui sont reliées entre elles afin de déterminer la corrélation entre elles. Pour qu'un ensemble de données soit considéré comme des données appariées, ces deux valeurs de données doivent être attachées ou liées l'une à l'autre et non considérées séparément.

L'idée de données appariées contraste avec l'association habituelle d'un nombre à chaque point de données comme dans d'autres ensembles de données quantitatives en ce que chaque point de données individuel est associé à deux nombres, fournissant un graphique qui permet aux statisticiens d'observer la relation entre ces variables dans une population.

Cette méthode de données appariées est utilisée lorsqu'une étude espère comparer deux variables chez des individus de la population pour tirer une sorte de conclusion sur la corrélation observée. Lors de l'observation de ces points de données, l'ordre de l'appariement est important car le premier nombre est une mesure d'une chose tandis que le second est une mesure de quelque chose de complètement différent.

Exemple de données appariées

Pour voir un exemple de données appariées, supposons qu'un enseignant compte le nombre de devoirs que chaque élève a remis pour une unité particulière, puis associe ce nombre avec le pourcentage de chaque élève au test unitaire. Les paires sont les suivantes:

• Une personne qui a terminé 10 affectations a obtenu 95% à son test. (10, 95%)
• Une personne qui a terminé 5 affectations a obtenu 80% à son test. (5, 80%)
• Une personne qui a terminé 9 affectations a obtenu 85% à son test. (9, 85%)
• Une personne qui a terminé 2 devoirs a obtenu 50% sur son test. (2, 50%)
• Une personne qui a terminé 5 devoirs a obtenu 60% à son test. (5, 60%)
• Une personne qui a terminé 3 devoirs a obtenu 70% à son test. (3, 70%)

Dans chacun de ces ensembles de données appariées, nous pouvons voir que le nombre d'assignations vient toujours en premier dans la paire ordonnée tandis que le pourcentage gagné sur le test vient en second, comme on le voit dans la première instance de (10, 95%).

Bien qu'une analyse statistique de ces données puisse également être utilisée pour calculer le nombre moyen de devoirs effectués ou le score moyen au test, il peut y avoir d'autres questions à poser sur les données. Dans ce cas, l'enseignant souhaite savoir s'il existe un lien entre le nombre de devoirs remis et les performances du test, et l'enseignant devra conserver les données appariées afin de répondre à cette question..

Analyse des données appariées

Les techniques statistiques de corrélation et de régression sont utilisées pour analyser des données appariées dans lesquelles le coefficient de corrélation quantifie la proximité des données le long d'une ligne droite et mesure la force de la relation linéaire.

La régression, d'autre part, est utilisée pour plusieurs applications, y compris la détermination de la ligne qui convient le mieux à notre ensemble de données. Cette ligne peut ensuite, à son tour, être utilisée pour estimer ou prédire y valeurs pour les valeurs de X qui ne faisaient pas partie de notre ensemble de données d'origine.

Il existe un type spécial de graphique particulièrement adapté aux données appariées appelé nuage de points. Dans ce type de graphique, un axe de coordonnées représente une quantité des données appariées tandis que l'autre axe de coordonnées représente l'autre quantité des données appariées.

Un nuage de points pour les données ci-dessus aurait l'axe des x dénoter le nombre d'affectations retournées tandis que l'axe des y dénoterait les scores sur le test unitaire.