La signification de l'exclusion mutuelle dans les statistiques

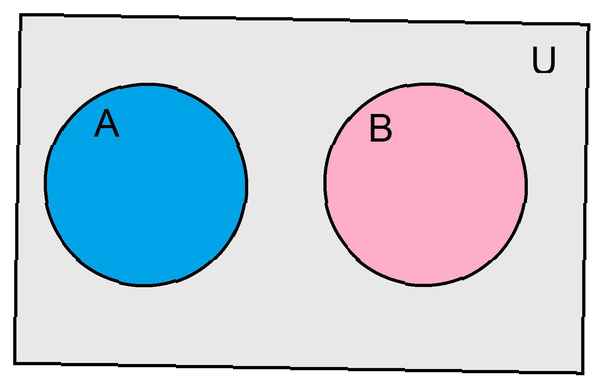
Il est probable que deux événements s'excluent mutuellement si et seulement si les événements n'ont pas de résultats communs. Si nous considérons les événements comme des ensembles, nous dirions que deux événements s'excluent mutuellement lorsque leur intersection est l'ensemble vide. Nous pourrions indiquer que les événements UNE et B s'excluent mutuellement par la formule UNE ∩ B = Ø. Comme pour de nombreux concepts de probabilité, quelques exemples aideront à donner un sens à cette définition.

Rolling Dice

Supposons que nous lançons deux dés à six faces et ajoutons le nombre de points affichés au-dessus des dés. L'événement consistant en "la somme est paire" est mutuellement exclusif de l'événement "la somme est impaire". La raison en est qu'il est impossible qu'un nombre soit pair et impair.

Maintenant, nous allons effectuer la même expérience de probabilité de lancer deux dés et d'ajouter les nombres affichés ensemble. Cette fois, nous considérerons l'événement consistant à avoir une somme impaire et l'événement consistant à avoir une somme supérieure à neuf. Ces deux événements ne s'excluent pas mutuellement.

La raison en est évidente lorsque nous examinons les résultats des événements. Le premier événement a des résultats de 3, 5, 7, 9 et 11. Le deuxième événement a des résultats de 10, 11 et 12. Puisque 11 est dans les deux, les événements ne s'excluent pas mutuellement..

Cartes à dessin

Nous illustrons plus loin avec un autre exemple. Supposons que nous tirions une carte d'un jeu standard de 52 cartes. Dessiner un cœur n'est pas mutuellement exclusif à l'événement de dessiner un roi. C'est parce qu'il y a une carte (le roi des coeurs) qui apparaît dans ces deux événements.

En quoi est-ce important

Il y a des moments où il est très important de déterminer si deux événements s'excluent mutuellement ou non. Savoir si deux événements s'excluent mutuellement influence le calcul de la probabilité que l'un ou l'autre se produise.

Revenez à l'exemple de la carte. Si nous tirons une carte d'un jeu de 52 cartes standard, quelle est la probabilité que nous ayons pioché un cœur ou un roi?

Tout d'abord, divisez cela en événements individuels. Pour trouver la probabilité que nous ayons dessiné un cœur, nous comptons d'abord le nombre de cœurs dans le jeu comme 13, puis nous divisons par le nombre total de cartes. Cela signifie que la probabilité d'un cœur est de 13/52.

Pour trouver la probabilité que nous ayons tiré un roi, nous commençons par compter le nombre total de rois, ce qui donne quatre, et ensuite diviser par le nombre total de cartes, qui est 52. La probabilité que nous ayons tiré un roi est 4/52.

Le problème est maintenant de trouver la probabilité de dessiner un roi ou un cœur. Voici où nous devons être prudents. Il est très tentant d'ajouter simplement les probabilités de 13/52 et 4/52. Ce ne serait pas correct car les deux événements ne s'excluent pas mutuellement. Le roi de cœur a été compté deux fois dans ces probabilités. Pour contrer le double comptage, nous devons soustraire la probabilité de dessiner un roi et un cœur, qui est 1/52. Par conséquent, la probabilité que nous ayons dessiné un roi ou un cœur est 16/52.

Autres utilisations mutuellement exclusives

Une formule connue sous le nom de règle d'addition donne un autre moyen de résoudre un problème tel que celui ci-dessus. La règle d'addition se réfère en fait à quelques formules qui sont étroitement liées les unes aux autres. Nous devons savoir si nos événements s'excluent mutuellement afin de savoir quelle formule d'addition est appropriée à utiliser.