Que sont les résidus?

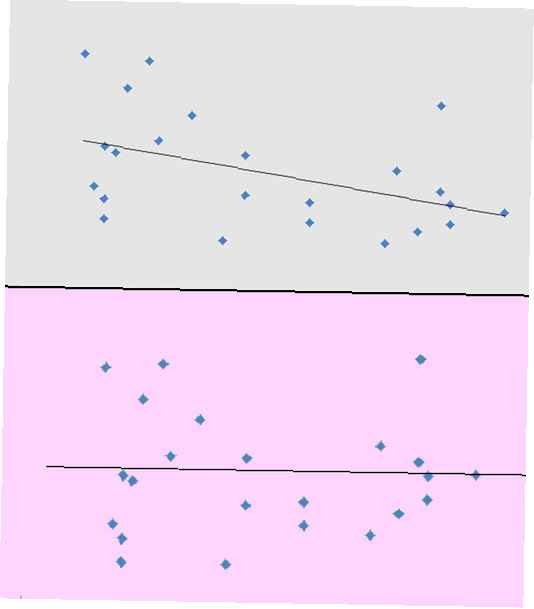
La régression linéaire est un outil statistique qui détermine l'adéquation d'une ligne droite avec un ensemble de données appariées. La ligne droite qui correspond le mieux à ces données est appelée la ligne de régression des moindres carrés. Cette ligne peut être utilisée de plusieurs façons. L'une de ces utilisations consiste à estimer la valeur d'une variable de réponse pour une valeur donnée d'une variable explicative. Liée à cette idée est celle d'un résidu.

Les résidus sont obtenus en effectuant une soustraction. Tout ce que nous devons faire est de soustraire la valeur prédite de y de la valeur observée de y pour un particulier X. Le résultat est appelé résiduel.

Formule pour les résidus

La formule pour les résidus est simple:

Résiduel = observé y - prédit y

Il est important de noter que la valeur prédite provient de notre droite de régression. La valeur observée provient de notre ensemble de données.

Exemples

Nous illustrerons l'utilisation de cette formule à l'aide d'un exemple. Supposons que l'on nous donne l'ensemble de données appariées suivant:

(1, 2), (2, 3), (3, 7), (3, 6), (4, 9), (5, 9)

En utilisant un logiciel, nous pouvons voir que la ligne de régression des moindres carrés est y = 2X. Nous l'utiliserons pour prédire les valeurs de chaque valeur de X.

Par exemple, lorsque X = 5, nous voyons que 2 (5) = 10. Cela nous donne le point le long de notre ligne de régression qui a un X coordonnée de 5.

Pour calculer le résidu aux points X = 5, nous soustrayons la valeur prédite de notre valeur observée. Depuis le y la coordonnée de notre point de données était de 9, ce qui donne un résidu de 9 - 10 = -1.

Dans le tableau suivant, nous voyons comment calculer tous nos résidus pour cet ensemble de données:

X	Observé y	Y prévu	Résiduel
1	2	2	0
2	3	4	-1
3	sept	6	1
3	6	6	0
4	9	8	1
5	9	dix	-1

Caractéristiques des résidus

Maintenant que nous avons vu un exemple, il y a quelques caractéristiques des résidus à noter:

• Les résidus sont positifs pour les points qui se situent au-dessus de la ligne de régression.
• Les résidus sont négatifs pour les points qui tombent sous la ligne de régression.
• Les résidus sont nuls pour les points qui tombent exactement le long de la ligne de régression.
• Plus la valeur absolue du résidu est élevée, plus le point est éloigné de la droite de régression.
• La somme de tous les résidus doit être nulle. Dans la pratique, parfois, cette somme n'est pas exactement nulle. La raison de cet écart est que les erreurs d'arrondi peuvent s'accumuler.

Utilisations des résidus

Il existe plusieurs utilisations pour les résidus. Une utilisation est de nous aider à déterminer si nous avons un ensemble de données qui a une tendance linéaire globale, ou si nous devrions envisager un modèle différent. La raison en est que les résidus aident à amplifier tout motif non linéaire dans nos données. Ce qui peut être difficile à voir en regardant un nuage de points peut être plus facilement observé en examinant les résidus et un tracé résiduel correspondant.

Une autre raison de considérer les résidus est de vérifier que les conditions d'inférence pour la régression linéaire sont remplies. Après vérification d'une tendance linéaire (en vérifiant les résidus), nous vérifions également la distribution des résidus. Afin de pouvoir effectuer l'inférence de régression, nous voulons que les résidus sur notre droite de régression soient distribués approximativement normalement. Un histogramme ou stemplot des résidus aidera à vérifier que cette condition est remplie.