Feuille de calcul pour l'inégalité de Chebyshev

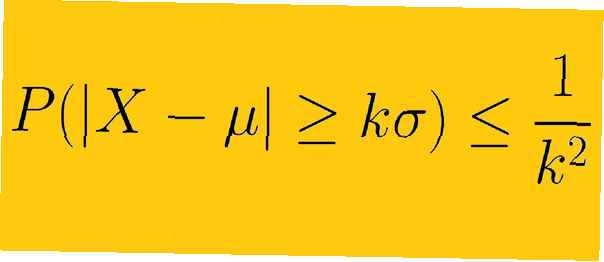
L'inégalité de Chebyshev indique qu'au moins 1 -1 /K² des données d'un échantillon doivent relever de K écarts-types de la moyenne, où K est tout nombre réel positif supérieur à un. Cela signifie que nous n'avons pas besoin de connaître la forme de la distribution de nos données. Avec seulement la moyenne et l'écart type, nous pouvons déterminer la quantité de données d'un certain nombre d'écarts types par rapport à la moyenne.

Voici quelques problèmes à pratiquer en utilisant l'inégalité.

Exemple 1

Une classe de deuxième année a une hauteur moyenne de cinq pieds avec un écart type d'un pouce. Au moins quel pourcentage de la classe doit être compris entre 4'10 ”et 5'2”?

Solution

Les hauteurs indiquées dans la plage ci-dessus se situent à moins de deux écarts-types de la hauteur moyenne de cinq pieds. L'inégalité de Chebyshev dit qu'au moins 1 - 1/2² = 3/4 = 75% de la classe est dans la plage de hauteur donnée.

Exemple # 2

Les ordinateurs d'une entreprise donnée durent en moyenne trois ans sans aucun dysfonctionnement matériel, avec un écart type de deux mois. Au moins quel pourcentage des ordinateurs durent entre 31 mois et 41 mois?

Solution

La durée de vie moyenne de trois ans correspond à 36 mois. Les délais de 31 mois à 41 mois sont chacun 5/2 = 2,5 écarts-types de la moyenne. Par l'inégalité de Chebyshev, au moins 1 - 1 / (2,5) 6² = 84% des ordinateurs durent de 31 mois à 41 mois.

Exemple # 3

Les bactéries dans une culture vivent pendant une durée moyenne de trois heures avec un écart type de 10 minutes. Au moins quelle fraction des bactéries vit entre deux et quatre heures?

Solution

Deux et quatre heures sont chacune à une heure de la moyenne. Une heure correspond à six écarts-types. Donc au moins 1 - 1/6² = 35/36 = 97% des bactéries vivent entre deux et quatre heures.

Exemple # 4

Quel est le plus petit nombre d'écarts-types par rapport à la moyenne que nous devons respecter si nous voulons nous assurer d'avoir au moins 50% des données d'une distribution?

Solution

Ici, nous utilisons l'inégalité de Chebyshev et travaillons en arrière. Nous voulons 50% = 0,50 = 1/2 = 1 - 1 /K². Le but est d'utiliser l'algèbre pour résoudre K.

On voit que 1/2 = 1 /K². Croisez multipliez et voyez que 2 =K². Nous prenons la racine carrée des deux côtés, et depuis K est un certain nombre d'écarts-types, nous ignorons la solution négative de l'équation. Cela montre que K est égal à la racine carrée de deux. Ainsi, au moins 50% des données se situent à environ 1,4 écart-type de la moyenne.

Exemple # 5

La ligne de bus n ° 25 prend en moyenne 50 minutes avec un écart type de 2 minutes. Une affiche promotionnelle pour ce système de bus indique que «95% du temps, la ligne de bus n ° 25 dure de ____ à _____ minutes». Quels nombres rempliriez-vous avec?