Les propriétés associatives et commutatives

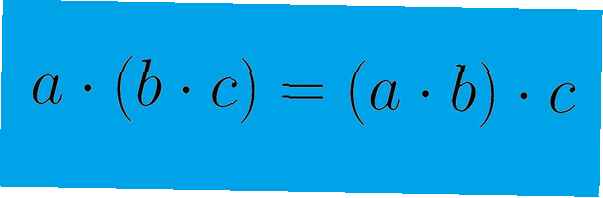
Il existe plusieurs propriétés mathématiques utilisées dans les statistiques et les probabilités; deux d'entre elles, les propriétés commutative et associative, sont généralement associées à l'arithmétique de base des entiers, des rationnels et des nombres réels, bien qu'elles apparaissent également dans les mathématiques plus avancées.

Ces propriétés - commutative et associative - sont très similaires et peuvent être facilement mélangées. Pour cette raison, il est important de comprendre la différence entre les deux.

La propriété commutative concerne l'ordre de certaines opérations mathématiques. Pour une opération binaire - une qui n'implique que deux éléments - cela peut être montré par l'équation a + b = b + a. L'opération est commutative car l'ordre des éléments n'affecte pas le résultat de l'opération. La propriété associative, quant à elle, concerne le regroupement d'éléments dans une opération. Cela peut être démontré par l'équation (a + b) + c = a + (b + c). Le regroupement des éléments, comme indiqué par les parenthèses, n'affecte pas le résultat de l'équation. Notez que lorsque la propriété commutative est utilisée, les éléments d'une équation sont réarrangé. Lorsque la propriété associative est utilisée, les éléments sont simplement regroupé.

Propriété commutative

En termes simples, la propriété commutative indique que les facteurs d'une équation peuvent être réarrangés librement sans affecter le résultat de l'équation. La propriété commutative concerne donc l'ordre des opérations, y compris l'addition et la multiplication des nombres réels, des nombres entiers et des nombres rationnels.

Par exemple, les nombres 2, 3 et 5 peuvent être additionnés dans n'importe quel ordre sans affecter le résultat final:

2 + 3 + 5 = 10

3 + 2 + 5 = 10

5 + 3 + 2 = 10

Les nombres peuvent également être multipliés dans n'importe quel ordre sans affecter le résultat final:

2 x 3 x 5 = 30

3 x 2 x 5 = 30

5 x 3 x 2 = 30

Cependant, la soustraction et la division ne sont pas des opérations pouvant être commutatives car l'ordre des opérations est important. Les trois chiffres ci-dessus ne peux pas, par exemple, être soustrait dans n'importe quel ordre sans affecter la valeur finale:

2 - 3 - 5 = -6

3 - 5 - 2 = -4

5 - 3 - 2 = 0