Raccourci de formule de somme des carrés

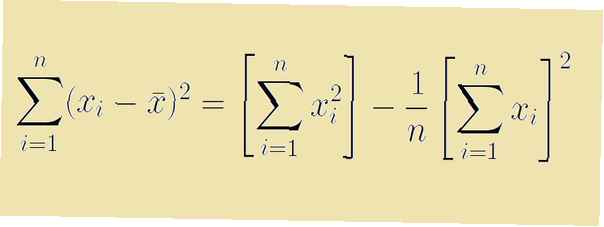
Le calcul d'une variance d'échantillon ou d'un écart-type est généralement exprimé sous forme de fraction. Le numérateur de cette fraction implique une somme des écarts au carré de la moyenne. En statistiques, la formule pour cette somme totale des carrés est

Σ (x_je - X)²

Ici, le symbole x̄ fait référence à la moyenne de l'échantillon, et le symbole Σ nous dit de additionner les différences au carré (x_je - x̄) pour tous je.

Bien que cette formule fonctionne pour les calculs, il existe une formule de raccourci équivalente qui ne nous oblige pas à calculer d'abord la moyenne de l'échantillon. Cette formule de raccourci pour la somme des carrés est

Σ (x_je²) - (Σ x_je)²/n

Ici la variable n fait référence au nombre de points de données dans notre échantillon.

Exemple de formule standard

Pour voir comment fonctionne cette formule de raccourci, nous allons considérer un exemple calculé à l'aide des deux formules. Supposons que notre échantillon soit 2, 4, 6, 8. La moyenne de l'échantillon est (2 + 4 + 6 + 8) / 4 = 20/4 = 5. Maintenant, nous calculons la différence de chaque point de données avec la moyenne 5.

• 2 - 5 = -3
• 4 - 5 = -1
• 6 - 5 = 1
• 8 - 5 = 3

Nous plaçons maintenant chacun de ces nombres et les additionnons ensemble. (-3)² + (-1)² + 1² + 3² = 9 + 1 + 1 + 9 = 20.

Exemple de formule de raccourci

Nous allons maintenant utiliser le même ensemble de données: 2, 4, 6, 8, avec la formule de raccourci pour déterminer la somme des carrés. Nous mettons d'abord en carré chaque point de données et les additionnons ensemble: 2² + 4² + 6² + 8² = 4 + 16 + 36 + 64 = 120.

L'étape suivante consiste à additionner toutes les données et à mettre cette somme au carré: (2 + 4 + 6 + 8)² = 400. On divise ceci par le nombre de points de données pour obtenir 400/4 = 100.

Nous soustrayons maintenant ce nombre à 120. Cela nous donne que la somme des écarts au carré est 20. C'est exactement le nombre que nous avons déjà trouvé dans l'autre formule.

Comment cela marche-t-il?

Beaucoup de gens accepteront simplement la formule à leur valeur nominale et ne savent pas pourquoi cette formule fonctionne. En utilisant un peu d'algèbre, nous pouvons voir pourquoi cette formule de raccourci est équivalente à la façon traditionnelle et traditionnelle de calculer la somme des écarts au carré.

Bien qu'il puisse y avoir des centaines, sinon des milliers de valeurs dans un ensemble de données réelles, nous supposerons qu'il n'y a que trois valeurs de données: x₁ , X₂, X₃. Ce que nous voyons ici pourrait être étendu à un ensemble de données contenant des milliers de points.

Nous commençons par noter que (x₁ + X₂ + X₃) = 3 x̄. L'expression Σ (x_je - X)² = (x₁ - X)² + (X₂ - X)² + (X₃ - X)².